
We get a lot of questions from readers. Sometimes our answers touch on things we haven’t fully explored in our articles. We want everyone to benefit from these nuggets of information so decided to post a series of Q&A articles which will highlight some interesting correspondence. Our first post covers three questions on the always popular topic of velocity.
Question 1: Using Velocity to Forecast Sales for a New Item
Q. What is the best way to determine the value (the $ opportunity) of new item placement in a new market or chain of stores, if item X is in Market REM but not yet in Market TA? Here’s my example:
Albertsons Southern TA does not stock Brand1 8oz Cheddar Cheese.
Albertsons Southern REM does stock Brand1 8oz Cheddar Cheese.
What is the opportunity in $ if Albertsons Southern TA stocks the item?
A. The simplest approach would be to pick a common/benchmark item that is in both markets and then look at how the target item performs versus that benchmark/common item in the REM and apply that ratio in the TA. Taking your example and applying made up numbers (click the table for a larger image):
I’m using the velocity metric Sales per Point of Distribution. Sales Per Point = Unit Sales / % ACV Distribution. You can’t apply that metric across markets because a “point of distribution” does not have the same value in both markets. But it is fine to compare velocity for two items within a market and then apply that relationship to a second market. Note: If you are reading this and don’t understand this paragraph, you should read our basic velocity post.
Back to our made up example. In Albertson Southern REM, Cheddar velocity is 17% higher than Swiss (187.5 / 160.0) so apply that to Albertson Southern TA and 61.5 is your starting velocity for Brand 1 8oz Cheddar (52.6 * 1.17). Now you need to make a distribution assumption. Do you want to go with 95%, which is the same as the Swiss item already carried? Check with your sales force to see the best assumption to make. Assuming 95%, your starting estimate for the new item would be 5,842 units (61.5 * 95).
You will also want to make some assumptions about cannibalization –– I often think it works best to apply a couple of scenarios e.g. potential volume if no cannibalization is best case and also show what volume might be if only 50% of the new item volume is incremental. You might make other adjustments based on known factors (e.g. you know customers in the TA tend to be especially crazy about cheddar based on other consumer research or how cheddar sales look for other brands).
Note to readers: See this post on how to identify where you might have the type of distribution opportunities referred to in this reader’s question.
Question 2: Calculating Category Velocity
Q2a. Do you have a view on the best way to calculate category velocity?
A. I don’t think there is a “best” way to calculate category velocity. It would depend on the goals of your analysis and also what data you have available. As with all attempts to aggregate distribution-based metrics, it’s important to understand the underlying components and implications. One important element is to think about whether your approximation is truly a total for the category or an average of the brands or items in the category. If the purpose of knowing this is to compare the velocity of brands or items to “the category” then you should use an average measure. If you are comparing entire categories across the store or department, you will need a more aggregate measure rather than an average measure.
Q2b. I have been proxying category velocity with the following calculation: multiplying Sales per Point of Distribution (SPP) of every brand within a category by that brand’s sales, summing this for all brands in the category, and dividing by total sales in the category. Does this make any sense? Is it useful for comparison? Sometimes this calculation produces odd results, such as a category velocity that is higher than all major brands in the category.
Note to Readers: I have created an example to illustrate what my correspondent was doing in their analysis: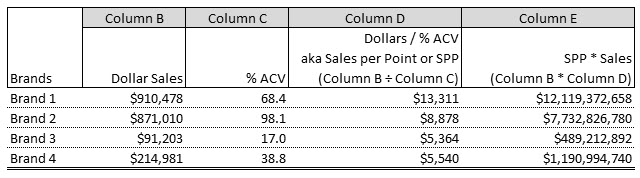
Category Velocity = Sum of Column B (Dollar Sales) ÷ Sum of Column E (SPP * Sales) = $21,532,407,070 ÷ $2,087,672 = $10,314
A. Your “category velocity” is a weighted average SPP at the brand level and your calculation sounds correct. In the cases where your average is higher than all the major brands, I would look at the underlying data and try to see why that is happening and make sure it is correct and logical given the specifics of that category. I’m sure there are situations where that would happen (maybe if you have a certain mix of national and regional brands where the regional brands have extremely high sales rates or the “major brands” aren’t that dominant) but I’d double check it if I saw that in my data because it is a little surprising. Often SPP will be very high for very small brands. Your weighting should take care of that (versus taking a straight average) but maybe something is going haywire.
One thing for you to consider is whether you want to use SPP or sales per TDP for this calculation. SPP will favor brands with more items in distribution. Some analysts would recommend using sales per TDP for just this reason, since the point of a velocity measure is to reduce the influence of distribution.
Note to Readers: If you do not have data where % ACV is calculated at the brand level (if you are a Nielsen Byzzer client, for example) you would have to use Sales per TDP in my correspondent’s category velocity calculation. You cannot calculate a brand % ACV from UPC level data unless one of the UPC’s has 100% ACV (in that case you know that brand % ACV is 100%).
Question 3: Comparing Velocity Across Markets
Q. The brand I manage just launched a new product. We are currently testing it at a high-end retailer (Retailer T) and want to see how its velocity compares to a competitor. But Retailer T doesn’t carry this competitor. It is analytically acceptable to compare $ per MM ACV for this competitor at another retailer to $ per MM ACV for our new product at Retailer T?
A. Yes – it is valid to compare $ per MM ACV (also referred to as $ per Million) across markets. The $ per Million metric will adjust for retailer size in a way that other velocity metrics (like $ per Point of Distribution) will not. So, from a pure metric standpoint, it’s valid.
But I’d be careful to choose a comparison retailer that is as similar as possible in geography, demographics, etc. You might compare category $ per million or some other metric of category development (level of variety?) to find a banner you think is comparable. That will lead to the most valid comparison. This is one of the frustrations of syndicated data analysis. There are a lot of different things going on all at the same time in each market! It can be a real challenge to make causally valid comparisons, even when your metrics and calculations are technically correct.
If you enjoyed this article, subscribe to future posts via email. We won’t share your email address with anyone.


Leave a Reply